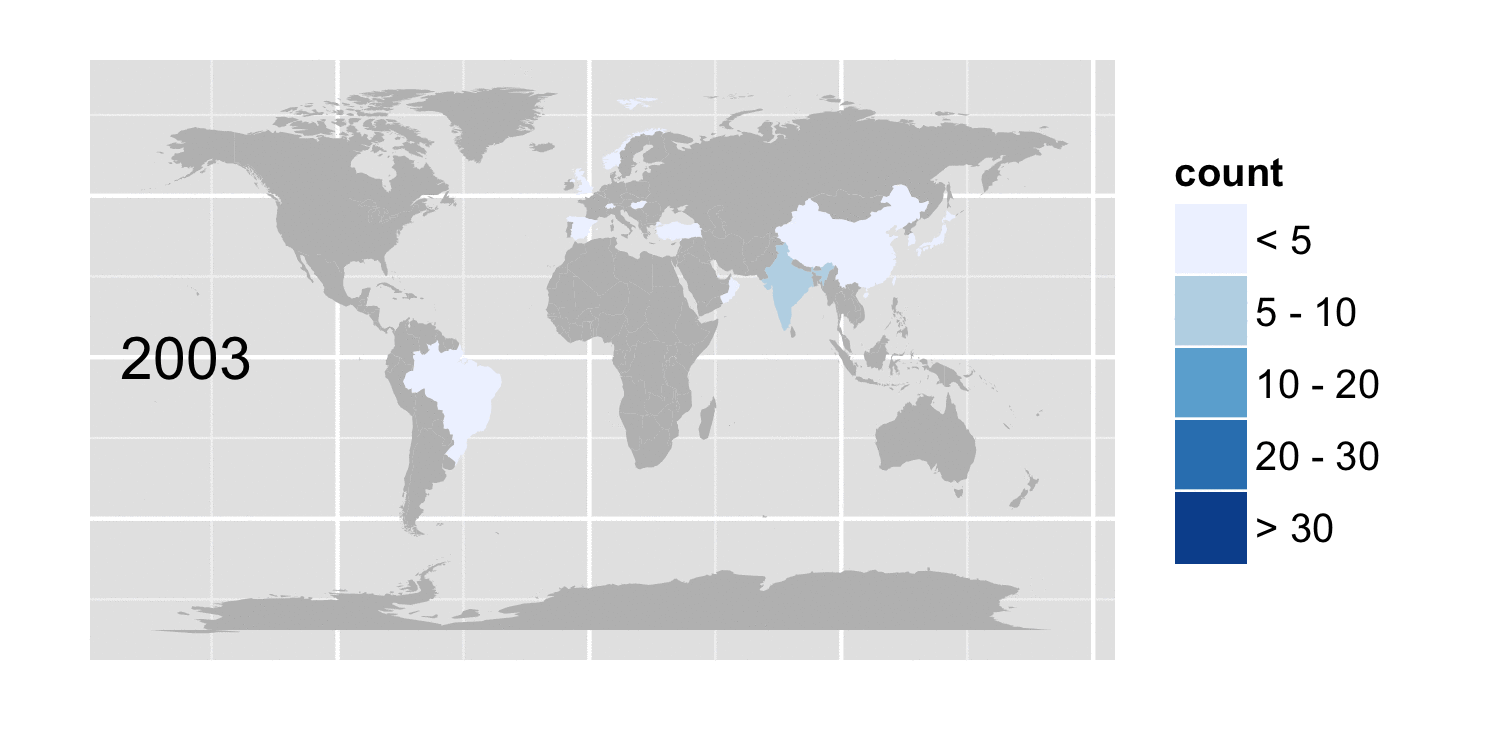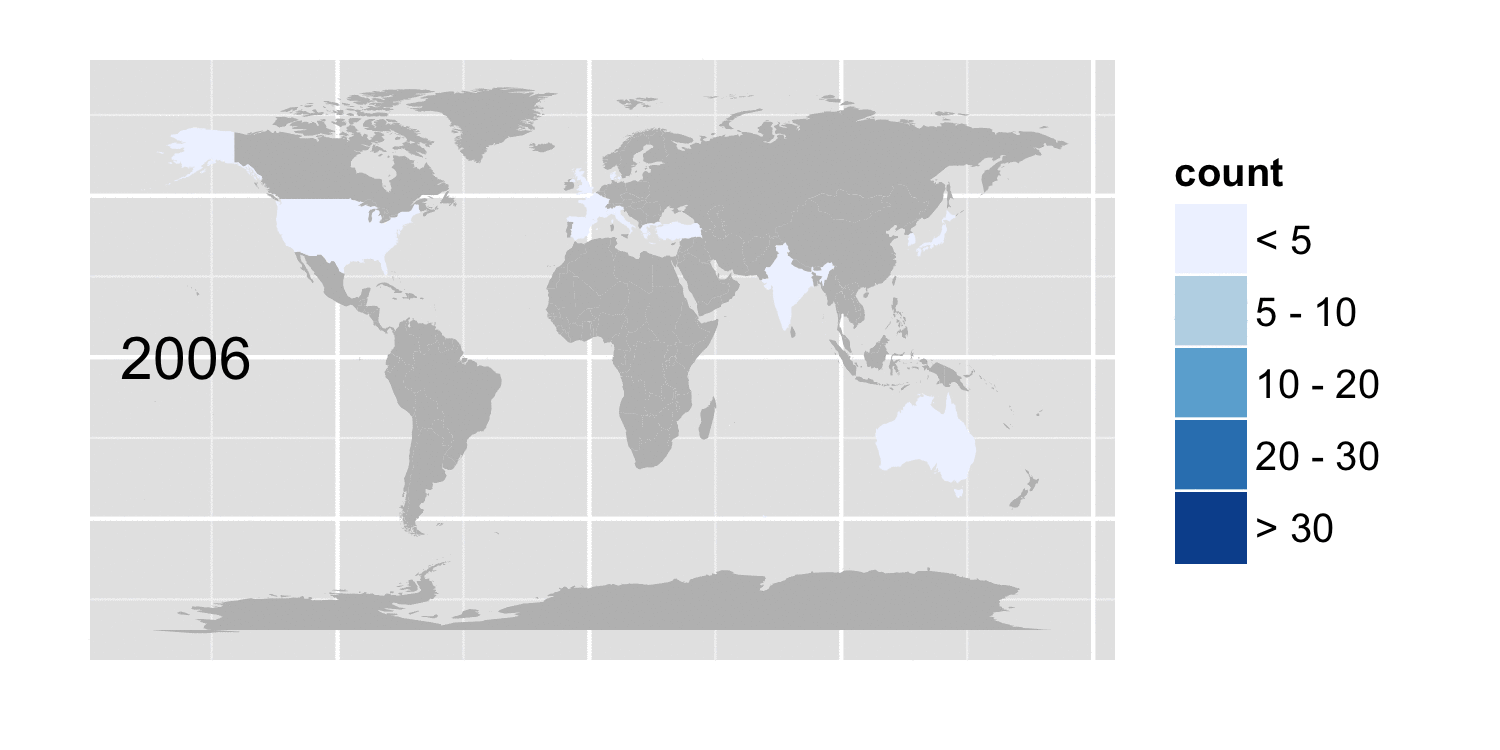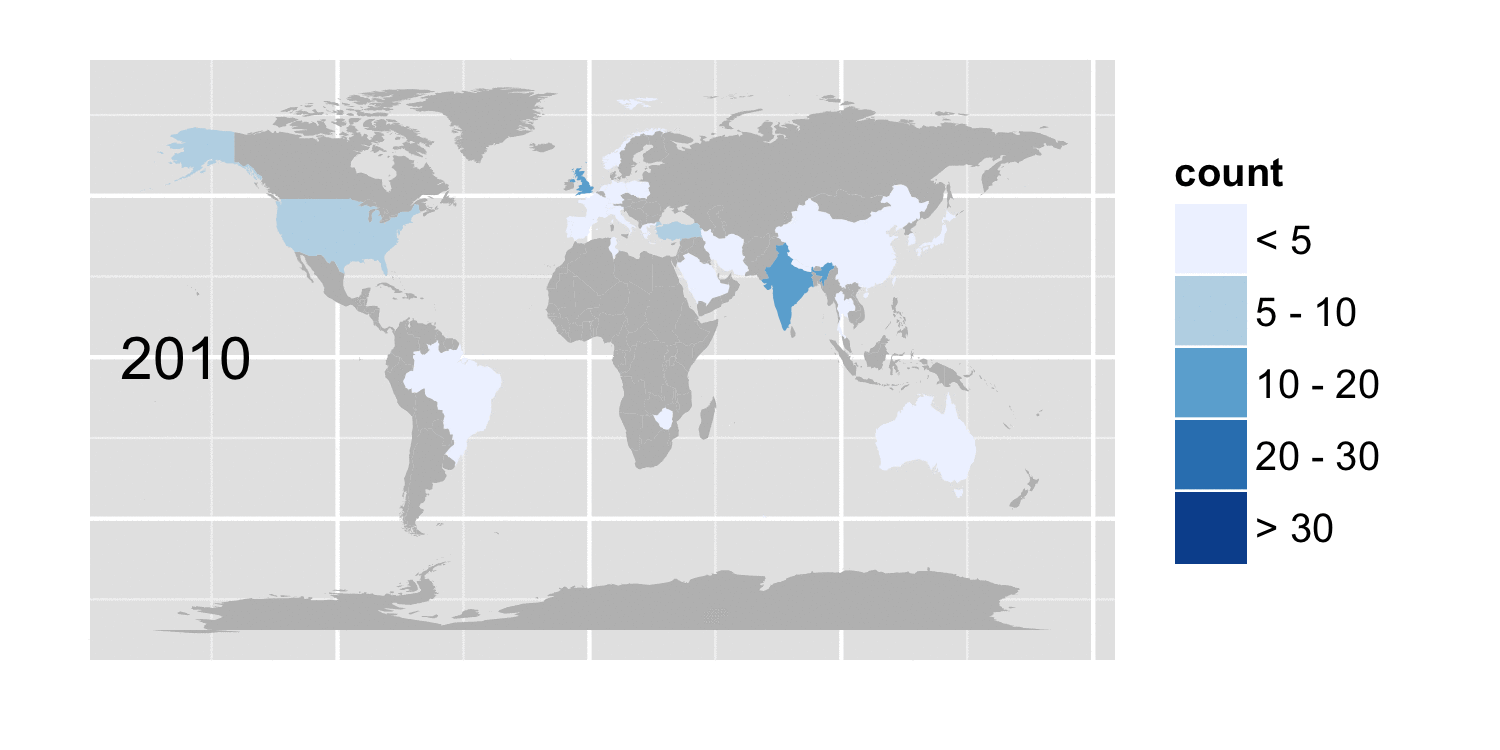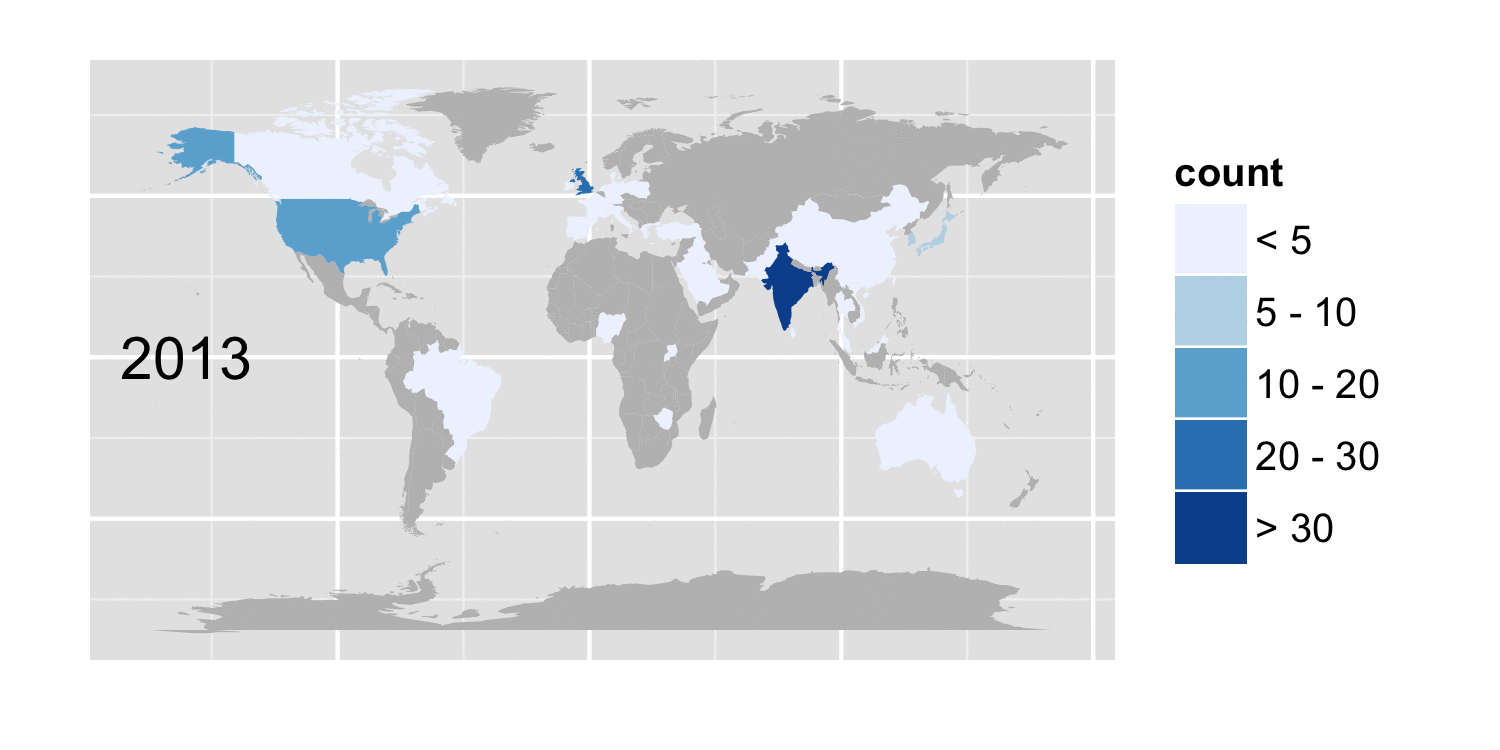
I came across a recent paper from the Tropsha group that discusses the issue of modelability – that is, can a dataset (represented as a set of computed descriptors and an experimental endpoint) be reliably modeled. Obviously the definition of reliable is key here and the authors focus on a cross-validated classification accuracy as the measure of reliability. Furthermore they focus on binary classification. This leads to a simple definition of modelability – for each data point, identify whether it’s nearest neighbor is in the same class as the data point. Then, the ratio of number of observations whose nearest neighbor is in the same activity class to the number observations in that activity class, summed over all classes gives the MODI score. Essentially this is a statement on linear separability within a given representation.
The authors then go show a pretty good correlation between the MODI scores over a number of datasets and their classification accuracy. But this leads to the question – if one has a dataset and associated modeling tools, why compute the MODI? The authors state
we suggest that MODI is a simple characteristic that can be easily computed for any dataset at the onset of any QSAR investigation
I’m not being rigorous here, but I suspect for smaller datasets the time requirements for MODI calculations is pretty similar to building the models themselves and for very large datasets MODI calculations may take longer (due to the requirement of a distance matrix calculation – though this could be alleviated using ANN or LSH). In other words – just build the model!
Another issue is the relation between MODI and SVM classification accuracy. The key feature of SVMs is that they apply the kernel trick to transform the input dataset into a higher dimensional space that (hopefully) allows for better separability. As a result MODI calculated on the input dataset should not necessarily be related to the transformed dataset that is actually operated on by the SVM. In other words a dataset with poor MODI could be well modeled by an SVM using an appropriate kernel.
The paper, by definition, doesn’t say anything about what model would be best for a given dataset. Furthermore, it’s important to realize that every dataset can be perfectly predicted using a sufficiently complex model. This is also known as an overfit model. The MODI approach to modelability avoids this by considering a cross-validated accuracy measure.
One application of MODI that does come to mind is for feature selection – identify a descriptor subset that leads to a predictive model. This is justified by the observed correlation between the MODI scores and the observed classification rates and would avoid having to test feature subsets with the modeling algorithm itself. An alternative application (as pointed out by the authors) is to identify subsets of the data that exhibit a good MODI score, thus leading to a local QSAR model.
More generally, it would be interesting to extend the concept to regression models. Intuitively, a dataset that is continuous in a given representation should have a better modelability than one that is discontinuous. This is exactly the scenario that can be captured using the activity landscape approach. Sometime back I looked at characterizing the roughness of an activity landscape using SALI and applied it to the feature selection problem – being able to correlate such a measure to predictive accuracy of models built on those datasets could allow one to address modelability (and more specifically, what level of continuity should a landscape present to be modelable) in general.