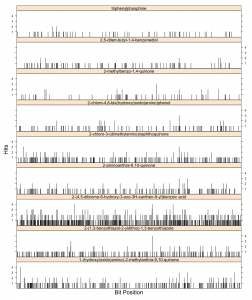
In my previous post I looked at how many collisions in bit positions were observed when generating hashed fingerprints (using the CDK 1024-bit hashed fingerprint and the Java hashCode method). I summarized the results in the form of “bit collision plots” where I plotted the number of times a bit was set to 1 versus the bit position (for a given molecule). As expected, for a series of molecules we observe a number of collisions in multiple bits. What was a little surprising was that even for a symmetric molecule like triphenylphosphine (i.e., a relatively small number of topologically unique paths), we observed collisions in two bits. So I decided to look into this case in a little more detail.
As I noted, collisions could occur if a) different paths get hashed to the same int or b) two different hashes lead to the same random number. Modifying the Fingerprinter code, I was able to generate the list of paths calculated for triphenylphosphine, the hash code for each path and the bit position that was generated for that hash code. The data (hash value, path, bit position) is given below.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| -662168118 P-C:C-H 3
-1466409134 H-C:C-P-C:C:C 58
1279033458 C:C:C:C:C-P-C:C:C 78
1434821739 H-C:C:C:C:C:C 80
-429128489 C:C:C:C-P-C 85
-1779215129 C:C:C:C:C 95
-245205916 H-C:C:C-P-C:C:C:C 97
-475263438 C:C:C:C:C:C-P-C:C 111
-1466409532 H-C:C-P-C:C-H 114
1434821341 H-C:C:C:C:C-H 142
-428753296 C:C:C:C:C:C 161
-245206314 H-C:C:C-P-C:C:C-H 161
1730724873 H-C:C:C-P-C 167
43327460 H-C:C:C:C:C-P-C:C 180
1731099668 H-C:C:C:C-H 180
886716569 H-C:C:C:C 182
-1406488727 C:C:C:C:C-P-C:C 191
78342 P-C 193
1731100066 H-C:C:C:C:C 211
63670037 C:C:C 213
178815835 H-C:C:C:C:C-P-C 224
179190630 H-C:C:C:C:C:C-H 230
-469902821 H-C:C-P-C:C:C:C 244
1057365278 C:C:C:C 253
-181369445 H-C:C:C:C-P-C:C 266
1056990085 C:C-P-C 300
886341376 H-C:C-P-C 333
827737424 H-C:C:C 390
-912402715 P-C:C:C:C:C-H 406
1572927053 H-C:C:C-P-C:C-H 421
1434446546 H-C:C:C:C-P-C 440
403512740 H-C:C:C:C:C:C-P-C 442
827737026 H-C:C-H 448
1572927451 H-C:C:C-P-C:C:C 458
-645296786 P-C:C:C:C:C:C-H 493
-688017645 P-C:C:C-H 503
-763796814 C:C:C:C-P-C:C:C:C 512
66252 C:C 574
75288527 P-C:C 600
-605043036 H-C:C-P-C:C:C:C:C 604
1074261266 H-C:C:C-P-C:C 629
-789313769 C:C:C-P-C:C 639
-2139775602 C:C-P-C:C 675
1370539593 H-C:C-P-C:C 698
284569632 C:C:C:C:C-P-C 702
1797624356 H-C:C:C:C-P-C:C:C 710
63294844 C-P-C 719
-912402317 P-C:C:C:C:C:C 725
72 H 741
67 C 742
80 P 744
-1779590322 C:C:C-P-C 762
1797623958 H-C:C:C:C-P-C:C-H 774
347808169 C:C:C:C-P-C:C:C 788
-688017247 P-C:C:C:C 815
240390684 P-C:C:C:C-H 834
-75615648 C:C:C:C-P-C:C 859
240391082 P-C:C:C:C:C 866
886716171 H-C:C:C-H 888
67900359 H-C:C 951
-1046303447 C:C:C:C:C:C-P-C 957
-662167720 P-C:C:C 969
70654 H-C 971
1678681248 C:C:C-P-C:C:C 979 |
First, all the hash codes are unique. So clearly the issue lies in the RNG and indeed, we see the following two paths being mapped to the same random integer.
1
2
| -428753296 C:C:C:C:C:C 161
-245206314 H-C:C:C-P-C:C:C-H 161 |
Does this mean that the two hash values, when used as seeds to the RNG give the same sequence of random ints? Using the code below
1
2
3
4
5
| Random rng1 = new Random(-428753296);
Random rng2 = new Random(-245206314);
for (int i = 0; i < 5; i++) {
System.out.println(rng1.nextInt(1024) + " " + rng2.nextInt(1024));
} |
we generate the first five random integers and we see that they match at the first value but then differ.
1
2
3
4
5
| 161 161
846 40
317 885
461 535
448 982 |
This suggests that instead of using the first random integer from the RNG seeded by a hash value, we use the second random integer. Modifying the code to do this still gives collisions in two bits. Once again, looking at the paths, hashes and bit positions, we see that now, two different paths get mapped to the same bit position.
1
2
| 886341376 H-C:C-P-C 686
1434821341 H-C:C:C:C:C-H 686 |
As before, we look at the sequence of random ints obtained from RNG’s seeded using these hash values. The resultant sequence looks like:
1
2
3
4
5
| 333 142
686 686
905 1022
70 571
177 384 |
So now, the two sequences match at the second value. OK, so what happens if we take the third value from the sequence and use that as a bit position? We get exactly the same behavior (collisions at two bit positions), except that now, when we look at the sequence of random int’s they match at the third value.
This behavior seems a little strange to me – as if there is a pair of seeds such that the “trajectory” of the sequences generated using those seeds will always (?) intersect at a certain point (where point actually corresponds to the n’th element of the sequences).
May be this is a property of random sequences? Or a feature of the Java RNG. I’d love to hear if anybody has insight into this behavior.